Physics:Alpha-particle spectroscopy

Short description: Quantitative measurement of the energy of alpha particles

For gamma ray measurement, see gamma spectroscopy. For beta particle detection, see liquid scintillation counting.

Alpha spectrometry (also known as alpha(-particle) spectroscopy) is the quantitative study of the energy of alpha particles emitted by a radioactive nuclide that is an alpha emitter.

As emitted alpha particles are mono-energetic (i.e. not emitted with a spectrum of energies, such as beta decay) with energies often distinct to the decay they can be used to identify which radionuclide they originated from.

Experimental methods

Example of how different paths of emitted mono-energetic alpha particles would lose energy and therefore cause signal broadening on the line spectrum. All paths lose energy to the air and detector window. Longer paths lose more energy. Paths iii & iv also show loss of energy passing through the source material itself. The red arrows indicate the magnitude of energy the particle is detected with.

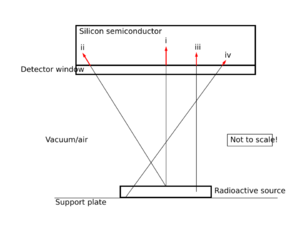
Counting with a source deposited onto a metal disk

It is common to place a drop of the test solution on a metal disk which is then dried out to give a uniform coating on the disk. This is then used as the test sample. If the thickness of the layer formed on the disk is too thick then the lines of the spectrum are broadened to lower energies. This is because some of the energy of the alpha particles is lost during their movement through the layer of active material.

Liquid scintillation

An alternative method is to use liquid scintillation counting (LSC), where the sample is directly mixed with a scintillation cocktail. When the individual light emission events are counted, the LSC instrument records the amount of light energy per radioactive decay event. The alpha spectra obtained by liquid scintillation counting are broaden because of the two main intrinsic limitations of the LSC method: (1) because the random quenching reduces the number of photons emitted per radioactive decay, and (2) because the emitted photons can be absorbed by cloudy or coloured samples (Lambert-Beer law). The liquid scintillation spectra are subject to Gaussian broadening, rather than to the distortion caused by the absorption of alpha-particles by the sample when the layer of active material deposited onto a disk is too thick.

Alpha spectra

Intensity against alpha energy for four isotopes, note that the line width is narrow and the fine details can be seen

Intensity against alpha energy for four isotopes, note that the line width is wide and some of the fine details can not be seen. This is for liquid scintillation counting, where random effects cause a variation in the number of visible photons generated per alpha decay

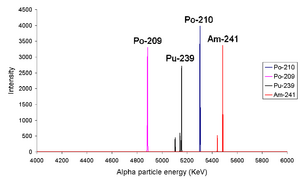
From left to right the peaks are due to ²⁰⁹Po, ²³⁹Pu, ²¹⁰Po and ²⁴¹Am. The fact that isotopes such as ²³⁹Pu and ²⁴¹Am have more than one alpha line indicates that the (daughter) nucleus can be in different discrete energy levels.

Calibration: MCA does not work on energy, it works on voltage. To relate the energy to voltage one must calibrate the detection system. Here different alpha emitting sources of known energy were placed under the detector and the full energy peak is recorded.

Measurement of thickness of thin foils: Energies of alpha particles from radioactive sources are measured before and after passing through the thin films. By measuring difference and using SRIM we can measure the thickness of thin foils.

Kinematics of alpha decay

The decay energy, Q (also called the Q-value of the reaction), corresponds to a disappearance of mass.

For the alpha decay nuclear reaction: [math]\ce{ ^{A}_{Z}P -> ^{(A-4)}_{(Z-2)}D + \alpha }[/math], (where P is the parent nuclide and D the daughter).

[math]\displaystyle{ Q{_\alpha} = (m_P - m_D - m_\alpha) \ c^2 }[/math], or to put in the more commonly used units: Q (MeV) = -931.5 ΔM (Da), (where ΔM = ΣM_products - ΣM_reactants).

When the daughter nuclide and alpha particle formed are in their ground states (common for alpha decay), the total decay energy is divided between the two in kinetic energy (T):

[math]\displaystyle{ Q_\alpha = T_\alpha + T_D }[/math]

The size of T is dependent on the ratio of masses of the products and due to the conservation of momentum (the parent's momentum = 0 at the moment of decay) this can be calculated:

[math]\displaystyle{ p_\alpha + p_D = 0 }[/math]

[math]\displaystyle{ T = 0.5mv^2 }[/math] and [math]\displaystyle{ p = mv }[/math], [math]\displaystyle{ \therefore p = \sqrt{2mT} }[/math]

[math]\displaystyle{ \begin{align} \sqrt{2m_\alpha T_\alpha} &= -\sqrt{2m_D T_D} \\[4pt] 2m_\alpha T_\alpha &= 2m_D T_D \\[4pt] \frac{m_\alpha}{m_D}T_\alpha &= T_D \end{align} }[/math]

[math]\displaystyle{ \begin{align} Q_\alpha &= T_\alpha + \frac{m_\alpha}{m_D}T_\alpha \\[4pt] &= T_\alpha\bigg(1 + \frac{m_\alpha}{m_D}\bigg) \\[4pt] &= T_\alpha\bigg(\frac{m_D}{m_D}+\frac{m_\alpha}{m_D}\bigg) \\[4pt] &= T_\alpha\bigg(\frac{m_D+m_\alpha}{m_D}\bigg) \\[4pt] \end{align} }[/math]

[math]\displaystyle{ \therefore T_\alpha = \frac{m_D}{m_P}Q_\alpha }[/math]

The alpha particle, or ⁴He nucleus, is an especially strongly bound particle. This combined with the fact that the binding energy per nucleon has a maximum value near A=56 and systematically decreases for heavier nuclei, creates the situation that nuclei with A>150 have positive Q_α-values for the emission of alpha particles.

For example, one of the heaviest naturally occurring isotopes, [math]\ce{ ^238U -> ^234Th + ^4He }[/math] (ignoring charges):

Q_α = -931.5 (234.043 601 + 4.002 603 254 13 - 238.050 788 2) = 4.2699 MeV

Note that the decay energy will be divided between the alpha-particle and the heavy recoiling daughter so that the kinetic energy of the alpha particle (T_α) will be slightly less:

T_α = (234.043 601 / 238.050 788 2) 4.2699 = 4.198 MeV, (note this is for the ^238gU to ^234gTh reaction, which in this case has the branching ratio of 79%). The kinetic energy of the recoiling ²³⁴Th daughter nucleus is T_D = (m_α / m_P) Q_α = (4.002 603 254 13 / 238.050 788 2) 4.2699 = 0.0718 MeV or 71.8 keV, which whilst much smaller is still substantially bigger than that of chemical bonds (<10 eV) meaning the daughter nuclide will break away from whatever chemical environment the parent had been in.

Example of how the alpha particle energy detected decreases with increasing air pressure (from right to left).

The recoil energy is also the reason that alpha spectrometers, whilst run under reduced pressure, are not operated at too low a pressure so that the air helps stop the recoiling daughter from moving completely out of the original alpha-source and cause serious contamination problems if the daughters are themselves radioactive.

The Qα‐values generally increase with increasing atomic number but the variation in the mass surface due to shell effects can overwhelm the systematic increase. The sharp peaks near A = 214 are due to the effects of the N = 126 shell.